The length of the perpendicular from the origin, on the normal to the curve, x 2 2 x y − 3 y 2 = 0 at the point (2, 2) is View Answer If x 2 4 x y 4 y 2 4 x c y 3 can be written as the product of two linear factors, then c =Get an answer for 'solve first grade ecuation with bernoulli dy/dx = (y^22xy)/x^2 general ecuation and particular when y(1)=1' and find homework help for other Math questions at eNotes2 In Squaring binomial, the middle term is ___ the product of the two terms in the binomial

Binomial Expansions In This Section Some Examples Obtaining The Coefficients Pdf Free Download
(x+y)2=x2+2xy+y2 example
(x+y)2=x2+2xy+y2 example-Solve the quadratic equation y 2x²y 2xy 3 = 0 🧮Solve the quadratic equation 2x² 2x 3 = 0 Quadratic Equation Calculator To solve a 2 nd order equation like ax² bx c = 0, enter or replace the coefficients a, b and c How to prove that F=(x^2y^2)i(2xyy)j is a conservative force Posted by By SK Math Expert No Comments Posted in Advanced Calculus , Algebra , Calculus , Mathematics , Vector Calculus




Simplifying Algebraic Expressions
Y(4) = 2 1 Rewriting the LHS in di erential form and factoring the RHS we getWe can try to factor x 2 −2xy−y 2 but we must do some rearranging first Change signs y 2 2xy−x 2 = − 1 k 2 Replace − 1 k 2 by c y 2 2xy−x 2 = c 1 the expression (x – y)^ 2xy y^ is an example of?
By taking LHS, (x – y) 2 = (x – y) (x – y) (x – y) 2 = x 2 – xy – xy y 2 (x – y) 2 = x 2 – 2xy y 2 LHS = RHS Hence, proved x 2 – y 2 = (x y) (x – y) By taking RHS and multiplying each term (x y) (x – y) = x 2 – xy xy – y 2 (x y) (x – y) = x 2 – y 2 Or x 2 – y 2 = (x y) (x – y) LHS = RHS Hence provedLHS = x 2 2xy y 2 LHS = RHS (x – y) 2 = x 2 y 2 – 2xy; $$ i^2 = j^2 = k^2 = 1 \\ ij = jk = ki = 1 $$ which sort of look like quaternions, but not quite In this case the factorisation becomes, $$ x^2 y^2 z^2 2xy 2yz 2zx = (ix jy kz)^2 $$ I didn't know if there was some algebra which obeyed these properties
Get an answer for '`2xy' y = x^3 x , y(4) = 2` Find the particular solution of the differential equation that satisfies the initial condition' and find homework help for other Math questionsSolve to get $$xy = \frac{1\pm\sqrt{18 y^2}}{2} $$ or $$x = y \frac{1\pm\sqrt{18 y^2}}{2} $$ Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at Teachoo



Http Www Maths Gla Ac Uk Cc 2a 2a Notes Chap1notes Sol Pdf




Binomial Expansions In This Section Some Examples Obtaining The Coefficients Pdf Free Download
Solution Our plan is to identify the real and imaginary parts of f, and then check if the CauchyRiemann equations hold for them We have f(z) = y 2xy i( x x2 y2) x2 y2 2ixy = x2 2xy y y2 i( xX 3 x y − 6 y Explanation First, rewrite by separating the fraction 6 x y 6 x 2 y 6 x y 1 8 x 2 y 2 − 6 x y x y 2 6x^24xy^23y^2/2xy 6 x 2 4 x y 2 − 3 y 2 / 2 x y It can be factored as x^2 y^2 = (xy)(xy) Notice that when you multiply (xy) by (xy) then the terms in xy cancel out, leaving x^2y^2 (xy)(xy) = x^2xyyxy^2 = x^2xyxyy^2 = x^2y^2 In general, if you spot something in the form a^2b^2 then it can be factored as (ab)(ab) For example 9x^216y^2 = (3x)^2(4y)^2 = (3x4y)(3x4y)




Implicit Differentiation



Pmt Physicsandmathstutor Com Download Maths A Level C4 Topic Qs Edexcel Set 1 C4 differentiation implicit differentiation Pdf
1 Let f(z) = y 2xyi( xx2 y2)z2 where z= xiyis a complex variable de ned in the whole complex plane For what values of zdoes f0(z) exist?Answer and Explanation 1 Become a Studycom member to unlock this answer!Dy/dx= (x^2 y^2)/ 2xy ( Homogenous) 1 f(x,y)= (x^2 y^2)/2xy, f ( kx,ky) = {(kx)^2 (ky^2)}/ 2kx ky = {(x^2 y^2)/2xy} k=0 (zero degree) Put y= vx =>dy/dx= v dv/dx 2 By 1 and 2 equation we get,




Dy Dx X 2 Y 2 2xy




Page Elements Of The Differential And Integral Calculus Granville Revised Djvu 277 Wikisource The Free Online Library
See the answer See the answer See the answer done loadingSOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sidesExample Factorize 9x 2 12xy 4y 2 Solution Step 1 Identify which identity can be applied in the expression We can apply (x y) 2 = x 2 2xy y 2 Step 2 Rearrange the expression so that it can appear in the form of the above identity 9x 2 12xy 4y 2 = (3x) 2 2 × 3x × 2y (2y) 2 Step 3 Once the expression is arranged in the form of the identity, write its factors



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf



Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver
Gradient x^2y^22xy, \at (1,2) \square!163 The Fundamental Theorem of Line Integrals One way to write the Fundamental Theorem of Calculus ( 721) is ∫b af ′ (x)dx = f(b) − f(a) That is, to compute the integral of a derivative f ′ we need only compute the values of f at the endpoints Something similar is$$x^22 x y y^2 x y 2 y^2 = 0$$ which may be further rewritten as $$(xy)^2(xy) 2 y^2 = 0$$ This is a quadratic in $xy$;




Schaum S Outline College Algebra Pdf Document



2
Depends what you mean If you mean the expressions exactly as you wrote them, then YES ^2= x^22xyy^2 if x=0 or y=0If x y = 3 and x^2 y^2 = 12, what is the value of 2xy?3 Aug/16 10 AM ET 3 PM BST 730 PM IST 5 Important Modifier Structures GMAT Most Probably Test You On



Www3 Nd Edu Zxu2 Triple Int16 8 Pdf




X Y 2 X2 2xy Y2 Brainly In
A) 9x3 5x27x2 b) 9 c) 7x2 d) 5x22x2 View Answer Answer d Explanation Polynomials only having three terms are called Trinomials Hence to find trinomial polynomial, we have to find polynomial which has three terms We can see that 5x 22x2 has three terms namely 5x 2, 2x and 2 Hence it is trinomial Similarly, polynomials only havingY' = 2/(y*(1x^2)) y′′−6y′9y=x^(−3)*e^(3x) (1x^2)dxy^2dy=0; Ex 95, 15 For each of the differential equations in Exercises from 11 to 15 , find the particular solution satisfying the given condition 2𝑥𝑦𝑦^2−2𝑥^2 𝑑𝑦/𝑑𝑥=0;𝑦=2 When 𝑥=1 Differential equation can be written 𝑎s 2𝑥𝑦𝑦^2−2𝑥^2 𝑑𝑦/𝑑𝑥=0 2𝑥𝑦𝑦^2= 2𝑥^2 𝑑𝑦/𝑑𝑥 2𝑥^2 𝑑𝑦/𝑑𝑥=2𝑥𝑦𝑦^2 𝑑𝑦/




Example 18 Show Curves Slope Of Tangent Is X2 Y2 2xy




The Graph Of The Equation 2x 2 Xy Y 2 4 Is The Tilted Ellipse Pictured Below Graph The Next Figure Is Not The Graph Of A Function Y F X However If
Answer to y' = 2xy^2;Consider x^ {2}y^ {2}xy22xy as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factorX^2y^2z^22xy2xz2yz WolframAlpha Rocket science?




The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C Youtube




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
Derivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;Learn with Tiger how to do x/(xy)y/(xy)(2xy)/(y^2x^2) fractions in a clear and easy way Equivalent Fractions,Least Common Denominator, ReducingWorked example Evaluating derivative with implicit differentiation 2y and then to X minus 2y times negative dy/dx that's just going to be negative 2x minus 2i or we could write that as 2 y minus 2 x times dy DX times dy/dx is equal to 1 plus dy DX is equal to 1 plus I'll do all my dy/dx is in orange now 1 plus dy DX so now there's a couple




Level Set Examples Math Insight




X2 2xy Y2 Dx X Y 2dy 0 Brainly In
Extended Keyboard Examples Upload Random (1x^2)y''2xy'2y=0 WolframAlpha Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionalsExample (c) Solve the equation (x2 y2 – y)dx xdy = 0 Example (d) Solve (y – xy²)dx (x x2y2)dy = 0 Exercises Except when the exercise indicates ofnerwise, find a set of solutions 1 y(2xy 1)dx – xdy = 0 2 y(y3 – x)dx x(y3 x)dy = 0 3Draw graph Edit expression Direct link to this page Value at x= Derivative Calculator Examples More derivative examples Please let us know if you have any suggestions on how to make Derivative Calculator better



Www Math Purdue Edu Shao92 Documents Examples1 9 Pdf




Using Completing Square To Simplify Surds Doc
Line integral example 2 (part 1) Google Classroom Facebook Twitter Email I'm going to have a path in the XY plane I'm going to start at the point I'm going to start right there at the point 2 comma 0 X is equal to 2 y 0 and I'm going to travel just like we did in the last video I'm going to travel along a circle but this time the circle2xy = 2 ⋅x⋅y 2 x y = 2 ⋅ x ⋅ y Rewrite the polynomial x2 2⋅x⋅yy2 x 2 2 ⋅ x ⋅ y y 2 Factor using the perfect square trinomial rule a2 2abb2 = (ab)2 a 2 2 a b b 2 = ( a b) 2, where a = x a = x and b = y b = y (xy)2 ( x y) 2There are a few of them, yeah Pick any real, distinct mathx, y/math Clearly then, math(xy)^2>0/math The square of a real number is never less than math0/math, and this will only equal math0/math if mathx=y/math, which is wh



16 1 2 Variables Separable Equations



1
Y = 1/(4 x^2) This problem has been solved!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Create your account View this answer (x23y2) dx−2xy dy = 0 ( x 2 3 y 2) d x − 2 x y d y



Scarpelli Assignment 2



Equation Of Tangent And Normal Using The Concept Of Differentiation
Explain why or why not using an example to support your answer I seem to be stuck Found 2 solutions by josgarithmetic, richwmiller Answer by josgarithmetic() (Show Source) You can put this solution on YOUR website!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Not a problem Unlock StepbyStep Extended Keyboard Examples



2




Implicit Differentiation Lesson 3 Studocu
Put the values of v which you let in point 2 and you will get your answer Now lets do the math Given that (x^2 y^2)dx 2xy dy =0;Find an answer to your question Solve (X^22xyy^2)(x1) 10Admission to the Carnival is $4 Each game played costs an additional $2Answer to Solve 2xy 6x (x^24)y'=0 By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask




4 1 Implicit Differentiation
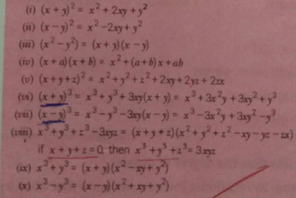



I X Y 2 X2 2xy Y2 Ii X Y 2 X2 2xy Y2 Iii X2 Scholr
Examples Example 1 Find an implicit solution of the IVP y0= xy 2y x 2 xy 3y x 3;(s t)2 (s t) Example 343 Let u= x2 2xy 2y3 where x= s2 lntand y= 2st3 Find @u @s and @u @t @u @s = @u @x @x @s @u @y @y @s = (2x 2y)(2slnt) 2x 6y2 2t3 = 2s2 lnt 4st3 (2slnt) 2s2 lnt 24s2t6 2t3 @u @t = @u @x @x @t @u @y @y @t = 2s2 lnt 4st3 2 s t 2s2 lnt 24s2t6 6st2 Example 344 Given z= f(x;y), x= r2 s2 and y= 2rs–nd @zIdentical expressions (one x^ two)y''2xy'= zero (1 plus x squared )y two strokes of the second (2nd) order plus 2xy stroke first (1st) order equally 0 (one plus x to the power of two)y two strokes of the second (2nd) order plus 2xy stroke first (1st) order equally zero




Mit Math Syllabus 10 3 Lesson 2 Polynomials




Ex 14 2 2 Vii Factorise X 2 2xy Y 2 Z 2 Ex 14 2
For example 1/2 and 2/4 are equivalent, y/(y1) 2 and (y 2 y)/(y1) 3 are equivalent as well To calculate equivalent fraction , multiply the Numerator of each fraction, by its respective MultiplierWhen we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2Algebra Examples Popular Problems Algebra Factor 2x^2xyy^2 2x2 − xy − y2 2 x 2 x y y 2 For a polynomial of the form ax2 bx c a x 2 b x c, rewrite the middle term as a sum of two terms whose product is a⋅c = 2⋅−1 = −2 a ⋅ c = 2 ⋅ 1 = 2 and whose sum is b = −1 b = 1




How Do I Prove That X 2 Y 2 X Y 2 2xy Geometrically Intuitively Mathematics Stack Exchange



Ocw Mit Edu Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang 14 Pdf



Www Sciencedirect Com Science Article Pii Sx Pdf Md5 4fdb47c005b02cccc568a29c7e6c Pid 1 S2 0 Sx Main Pdf




It Some Algebraic Identities Are Given Below Ti I X Y Scholr



Show That The Function Z 2x 2 2xy Y 2 2x 2y 2 Is Not Smaller Than 3 Youtube



Orion Math Iastate Edu Miriamc M165f18 3 7 Notes165 F18 Pdf



Double Integrals Over General Regions Page 2




Engineering Mathematics Notes



Http Www Math Jhu Edu Brown Courses F1815 Exampleproblems Exactode Pdf



Faculty Math Illinois Edu Franklan Math241 168 Stokesthm Pdf



Add Subtract And Simplify Fractions With Step By Step Math Problem Solver



10 Math Problems Addition And Subtraction Of Algebraic Fractions




Example 2 19 Let S Find The Expanded Form Of X Chegg Com



2




Solutions To Implicit Differentiation Problems



How To Draw Y 2 X 2 Interactive Mathematics



Consumer Theory



Integrate The Differential Equation Y X2 2y2 Xy Stumbling Robot




Ppt Polynomials Powerpoint Presentation Free Download Id



Xy1 Y X2y2 X2 2x Y1 2xy Xy4 0 Y1 Xy Chegg Com




Algorithm For X 2 Xy Y 2 Z 2 With The Solution 1 1 1 That Download Scientific Diagram



4 2 Implicit Differentiation




Presentation 12 Basic Algebra Basic Algebra Definitions A




Using Completing Square To Simplify Surds Doc
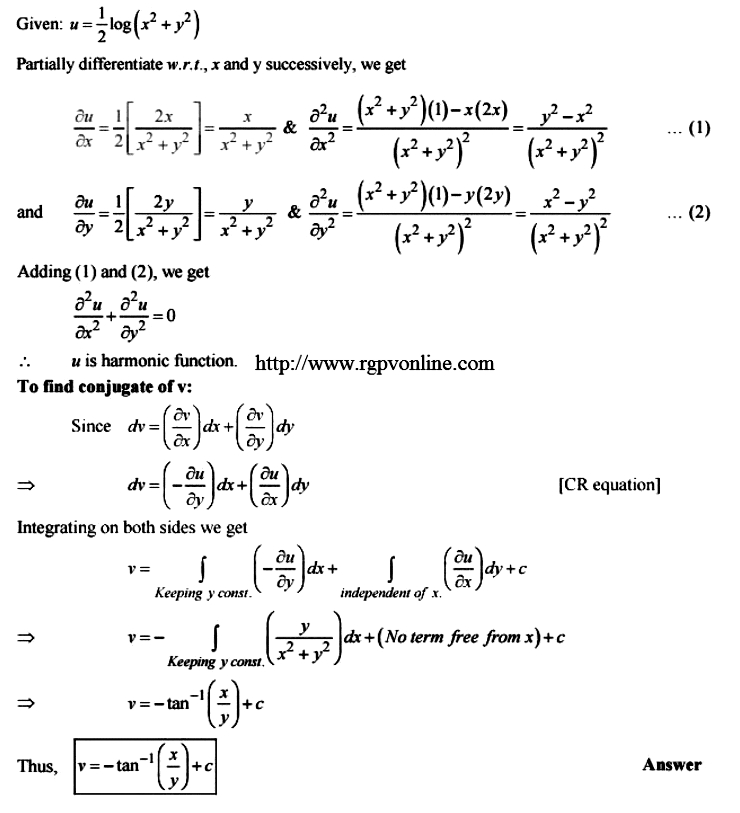



Show That The Following Function U 1 2 Log X 2 Y 2 Is Harmonic And Find Its Harmonic Conjugate Functions Mathematics 2 Question Answer Collection




2xy



2




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When



Exact Equations



X 2 2xy Y 2 X 2 Y 2 2x 2 Xy Y 2 X 2 Xy 2y 2 Youtube




How Do I Prove That X 2 Y 2 X Y 2 2xy Geometrically Intuitively Mathematics Stack Exchange




Graphs And Level Curves




Partial Derivative Examples Math Insight




Homogeneous Differential Equations



Www Math Drexel Edu Tolya Implicit Pdf
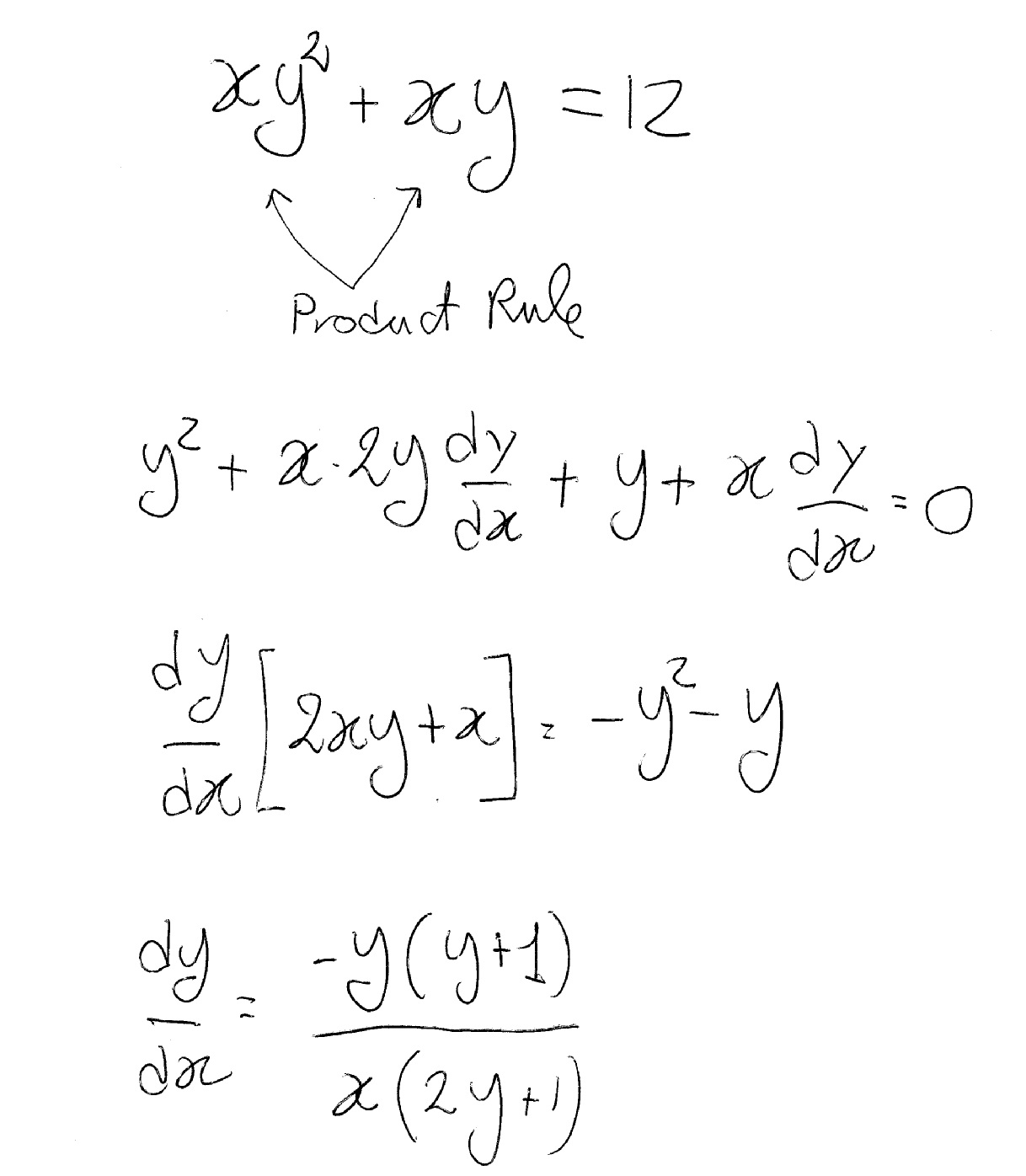



How Do You Differentiate Xy 2 Xy 12 Socratic




How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora



Q Tbn And9gcq8jeckpyefv6nxxng4iwjfl7hsluh Liz05p1lqjy Usqp Cau
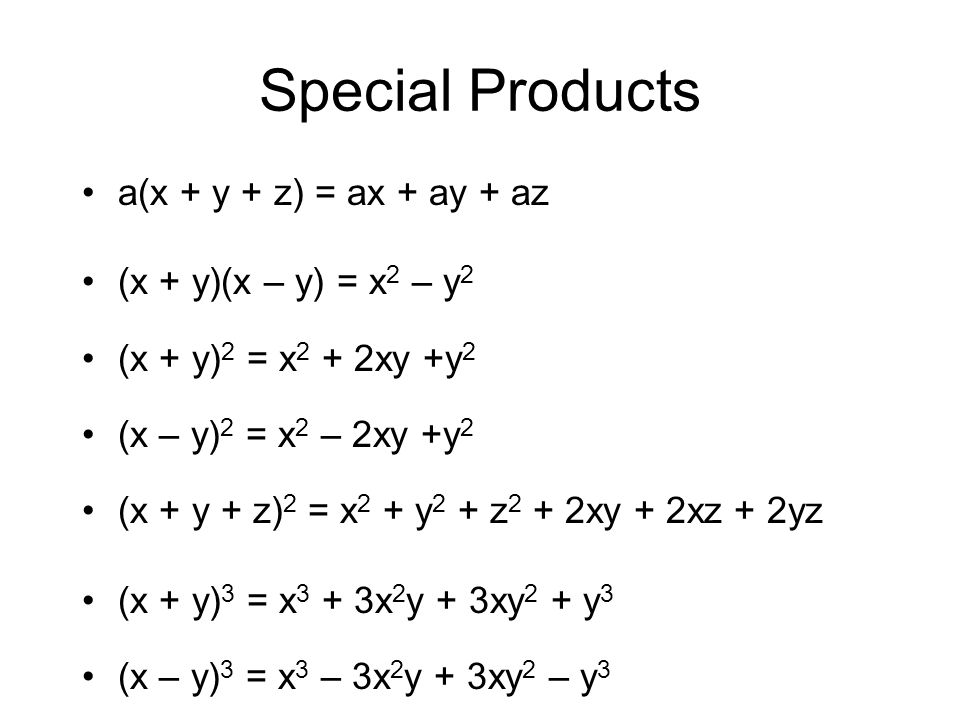



Special Products A X Y Z Ax Ay Az X Y X Y X 2 Y 2 X Y 2 X 2



Find The Sum Of X Y 2 Mathematics Topperlearning Com
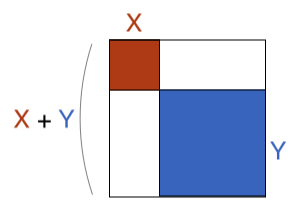



Does Sqrt X 2 Y 2 X Y Brilliant Math Science Wiki



1




2xy X 2 Y 2 X 2 Y 2 2xy Y 2 2xy X 2 A X 3 Y 3 2 B X 2 Y 2 3 C X 2 Y 2 3 D X 3 Y 3 2




Using The Binomial Theorem College Algebra




Simplifying Algebraic Expressions




Example 18 Show Curves Slope Of Tangent Is X2 Y2 2xy



Identity Vs Equation Acute Angel



Surface Area




Engineering Mathematics Notes




Is Math X Y 2 X 2 Y 2 Math Or Math X 2 2xy Y 2 Math Quora



Systems Of Linear Equations



How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora




Differential Equation 1st Order Reducible To Separable Forms 5 Of 7 Example 4 X 2y X 2 Xy Y 2 Youtube




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula



Www Math Uh Edu Bekki 2433 Su16 Notes Sn9 1 Pdf




How To Do Implicit Differentiation 7 Steps With Pictures




X Y 2 Solve Duparah




Factorisation Extra Help And Examples Studocu




How Does Wolfram Alpha Solve Systems Of Nonlinear Equations Math




Implicit Differentiation Advanced Example Video Khan Academy




P 4 Factoring Polynomials Ppt Video Online Download



Www Jstor Org Stable



Explicit And Implicit Functions




1 Consider The Curve Defined By X2 Xy Y2 27 A Write An




Factoring Algebraic Expressions Ppt Video Online Download



Scarpelli Assignment 2
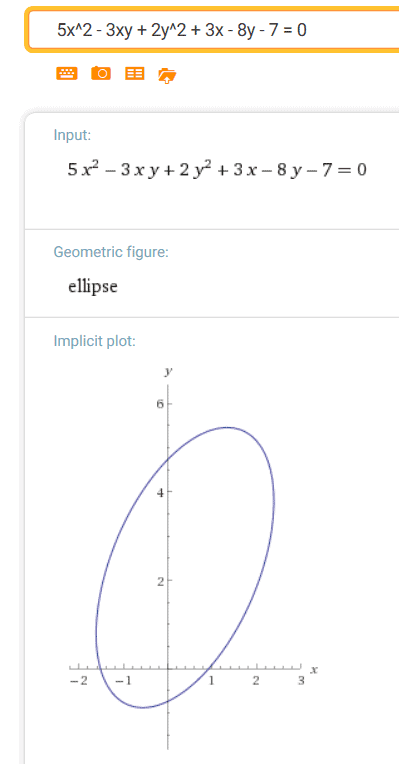



Identifying Conics By The Discriminant




Example 4 Consider The Function Z Rx Y X2 Chegg Com




Worked Example Implicit Differentiation Video Khan Academy




Get Answer Please Assist Me Thanks Use The Example Given However Change Transtutors




How Is Frac Dx Z X Y Frac Dy Z X Y Frac Dz X 2 Y 2 Equivalent To Frac Y Dx Xdy Zdz 0 Frac Xdx Ydy Zdz 0 Mathematics Stack Exchange




Answered Ca X Find F 1 X B Let F X K 2 Bartleby
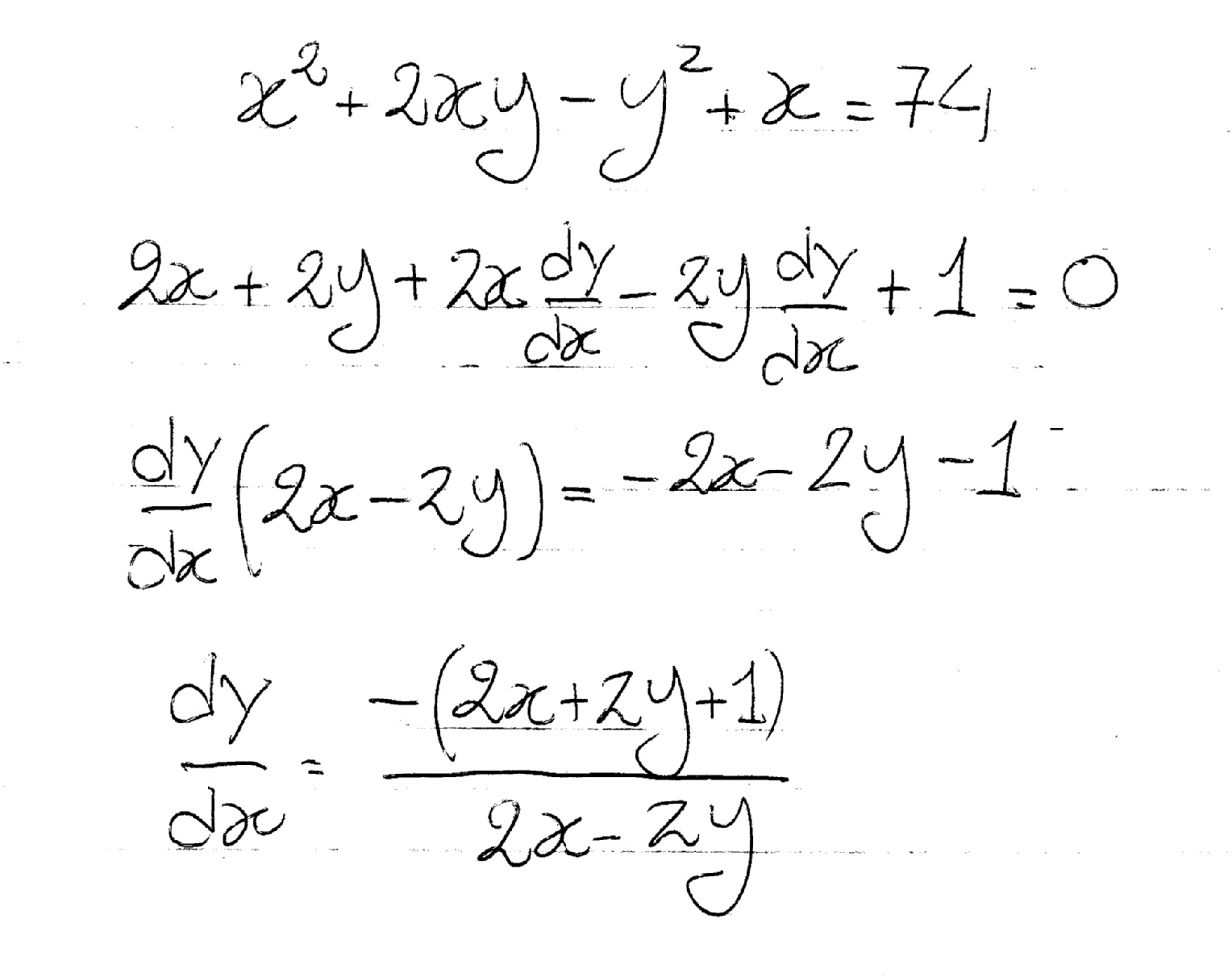



How Do You Differentiate X 2 2xy Y 2 X 74 Socratic



Search Q X 5e2 2b2xy 2by 5e2 Graph Tbm Isch



0 件のコメント:
コメントを投稿